Previously we announced that we discovered a novel way of cryptographically secure obfuscation of software. This article gives a brief illustrated overview of discovery. It also provides some practical examples based on existing implementation of technology in Eazfuscator.NET obfuscator for .NET platform.
Introduction
Obfuscation is relatively new field of cryptography and it often falls behind its older and bigger sibling - the data encryption. It's all about guarantees.
The data encryption guarantees that data remains unobservable unless an observer knows the key. The key is selected to be a large enough number (or blob of data) that is extremely hard (i.e. impossible) to brute force.
It's different when it comes to the code of a program. The code must remain observable in order to be executed by CPU. At the same time, a cryptographically secure obfuscation should make the code unobservable to an attacker.
What some obfuscators (specifically protectors) do is they encrypt the code and put the key right into resulting executable file. This serves the purpose only until the key is discovered by a decompiler or memory dumper. After that, the game is over - the full code becomes observable by an attacker. As you can see, not a whole lot of guarantees at all.
Extracting a key from executable file is billion of billions times simpler than brute forcing a 80 bit key used for encryption. An attacker wins by choosing the cheapest method.
The only technique contemporary obfuscators are good at is concealing the information. For example, Eazfuscator.NET does a good job on symbols by irreversibly renaming them. Removing the essential information is a great security measure. But the code is still there and it remains observable.
Another neat trick some obfuscators employ is code virtualization. It's achieved by translating the instructions of a target platform to instructions of a custom virtual machine. This gives solid results at the expense of code speed, but still the virtualized code remains somewhat observable. It is humanely possible to build a so-called devirtualizer that would obtain the original code of a program.
Indistinguishability Obfuscation
Indistinguishability obfuscation (IO) is a cryptographic primitive that provides a formal notion of program obfuscation. Informally, indistinguishability obfuscation hides the implementation of a program while still allowing users to run it.
That's exactly what we need in order to make the code unobservable by an attacker.
The definition of indistinguishability obfuscation has its roots at the notion of ciphertext indistinguishability which was later extended to a more general computational indistinguishability.
Homomorphic Encryption
At first, let's introduce a notion of program:
O = P(I)
where P denotes a program, I denotes its input and O stands for output.
The easiest way to look at this notion is to imagine that a program P is a Unix-like command line tool with input I in a form of stdin and output O in form of stdout.
In mathematical sense, program P may be much simpler than a full-blown application. For example, it can be just a single operation like multiplication.
The most intriguing candidate for indistinguishability obfuscation is Homomorphic Encryption (HE). Let's see how it works:
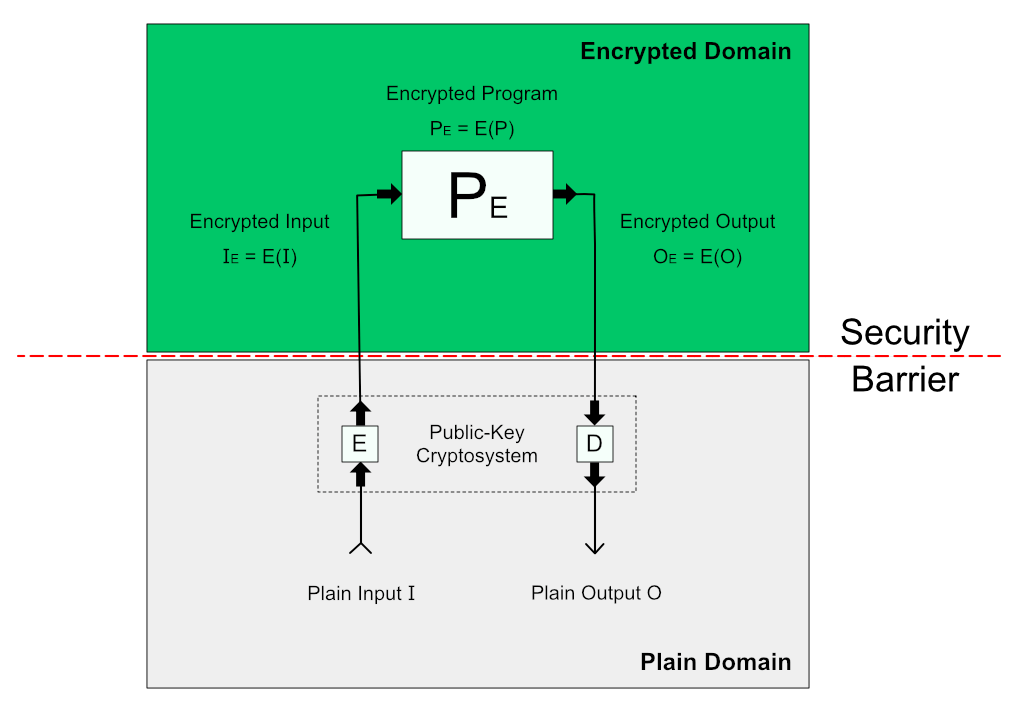Figure 1. Homomorphic encryption
Homomorphic encryption (HE) uses a public-key cryptosystem that provides E and D functions. Function E encrypts the data while D performs the inverse operation of decryption.
Now having those two functions we can write the program equation in homomorphically encrypted form by applying E to both sides of equation:
E(O) = E(P(E(I)))
Let's introduce three shortcut symbols to better understand what's going on:
PE = E(P); // encrypted program IE = E(I); // encrypted input OE = E(O); // encrypted output
This gives us a more concise view of HE program equation:
OE = PE(IE)
As you can see, the HE program PE solely works in encrypted domain, consuming encrypted input IE and producing encrypted output OE.
In this way, the homomorphic encryption can be used to move a computationally extensive work PE to an untrusted party through a remote communication channel. Since the untrusted party never receives the private key of asymmetric cryptosystem, it never knows what program or data are being evaluated.
This fact is denoted by the presence of a Security Barrier in the figure above. The whole HE scheme is secure as long as Encrypted Domain and Plain Domain are kept separated by the barrier.
But in software obfuscation, the security barrier is missing and PE should be able to work on unencrypted I and O.
Let's write down a corresponding program equation that reflects that:
O = D(PE(E(I)))
It goes just fine until D function is used to decrypt the output. This poses a fatal problem as function D can be used not only to decrypt the output, it can also be used to decrypt the encrypted program PE:
P = D(PE); // game over
In this way, the obfuscation of PE is getting thwarted, rendering the whole HE scheme without a security barrier useless.
A Seemingly Unsolvable Dilemma
The impossibility to build an indistinguishability obfuscation based on a general notion of homomorphic encryption that would be able to produce unencrypted output leads us to the root of a problem.
In data communication, participants are separated by natural barriers:
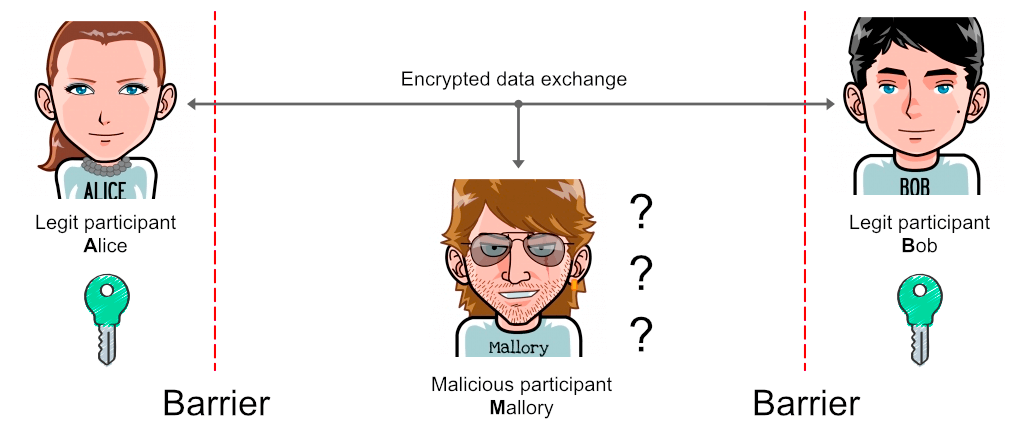Figure 2. Encrypted data communication
The presence of barriers is what makes data encryption feasible: an attacker is physically unable to retrieve the key and thus cannot decrypt the information.
In software obfuscation, all participants are located at the same security zone and every one of them has a physical access to an encryption key that is stored in software:
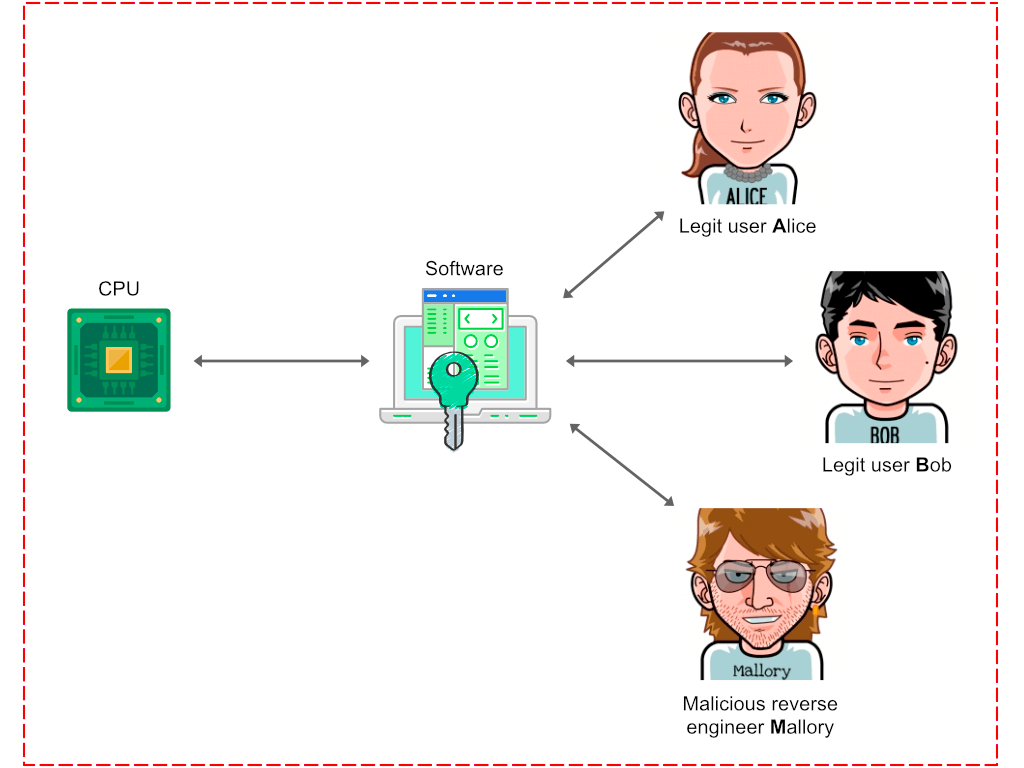Figure 3. The software obfuscation dilemma
The absence of security barrier between Mallory and an encryption key embedded in software renders all program obfuscation attempts useless as Mallory will always be able to decrypt it.
If we cease to embed a program encryption key in software, then we are safe from Mallory but CPU is not able to execute the program.
This represents a seemingly unsolvable dilemma of indistinguishability obfuscation of software.
Another name of this model is Virtual Black Box (VBB) obfuscation which was proven to be impossible by Barak et al. [Barak01]. The impossibility of VBB obfuscation means that we need to find a more relaxed model of obfuscation.
A Hint From The Book
On a cold fall of 2015, we stumbled upon important observation by Kris Kaspersky [Kris03, p. 567]:
The analysis of code can be thwarted successfully only by encrypting the program. However, the processor cannot directly execute the encrypted code. Therefore, it must be decrypted before control is passed to the program. If the key is contained within the program, the reliability of the protection is close to zero. ...
In general, protection consists of implementing a certain mathematical model in a program that is used to generate the key. Different branches of the program are encrypted using various keys. To work out the keys, it is necessary to know the state of the model at the moment control is passed to the corresponding branch of the program. The code is dynamically decrypted at run time. To decrypt it entirely, all possible states of the model need to be tried sequentially. If there are lots of them, which is easy to achieve, the reconstruction of all code will be practically impossible.
Kaspersky suggested a plausible obfuscation model. Let's call it a Conditional Indistinguishability Obfuscation (CiO).
The CiO model implies that conditional parts of a program remain indistinguishable until they are executed. Once they hit the execution path, they become uncovered by decryption and thus become observable to CPU (and to Mallory).
Since then, that brilliant idea never left our heads. It felt so powerful yet unreachable. An attacker cannot reconstruct the whole program as he only has access to the parts he can observe. And intuitively he cannot observe all the parts but... how to achieve that?
Kaspersky suggested to use "machine state" as the source of key material but it would be an inherently weak source due to the lack of entropy.
Indistinguishable Associative Array
Three years later, at fall of 2018, we became involved in construction of indistinguishable associative array. We needed it in order to protect the dispatch table of Eazfuscator.NET virtual machine from attacks based on static analysis.
Imagine a class IndistinguishableDictionary<long, long> that behaves just like the ordinary Dictionary<long, long> but with a twist: nobody is able to tell beforehand what association a dictionary holds unless they have a corresponding lookup key.
Ordinary Dictionary<long, long> can be enumerated, so all associations held by dictionary can be revealed:
foreach (var i in map)
Console.WriteLine("{0}={1}", i.Key, i.Value);
IndistinguishableDictionary does not allow enumeration by imposing a mathematical hurdle. The only operation it allows is lookup by a key:
value = map[key]
If attacker has no key, he cannot extract the association. The record in indistinguishable dictionary remains unobservable unless a proper lookup key is supplied.
To our surprise, we got a positive result. We were able to construct indistinguishable associative array with the help of homomorphic encryption. It was somewhat unpractical though as it required large keys with lots of bits, and that would lead to gigantic machine instructions.
And then, it hit us.
value = map[key] is just a specific case of a general notion of program O = P(I).
The program P by itself cannot contain a key suitable for black box encryption; but it has input I with lots of entropy, and that I is generally unknown to an attacker.
Program input I is the secret. This is a valid key material for cryptographic obfuscation.
On a closer inspection of Kris' Kaspersky work, we were able to finally identify some hints to this phenomenon [Kris03], albeit they were expressed not as clearly as we would generally prefer:
... Looking to [function] arguments allows the sequences sought to be caught in data streams, irrespective of how these sequences were obtained. For example, an authentication procedure expecting the password "MyGoodPassword" does not care where it came from (the keyboard, a remote terminal, a file, etc.).
More Detailed View on Software Obfuscation
Let's take a closer look at the detailed interaction diagram between participants:
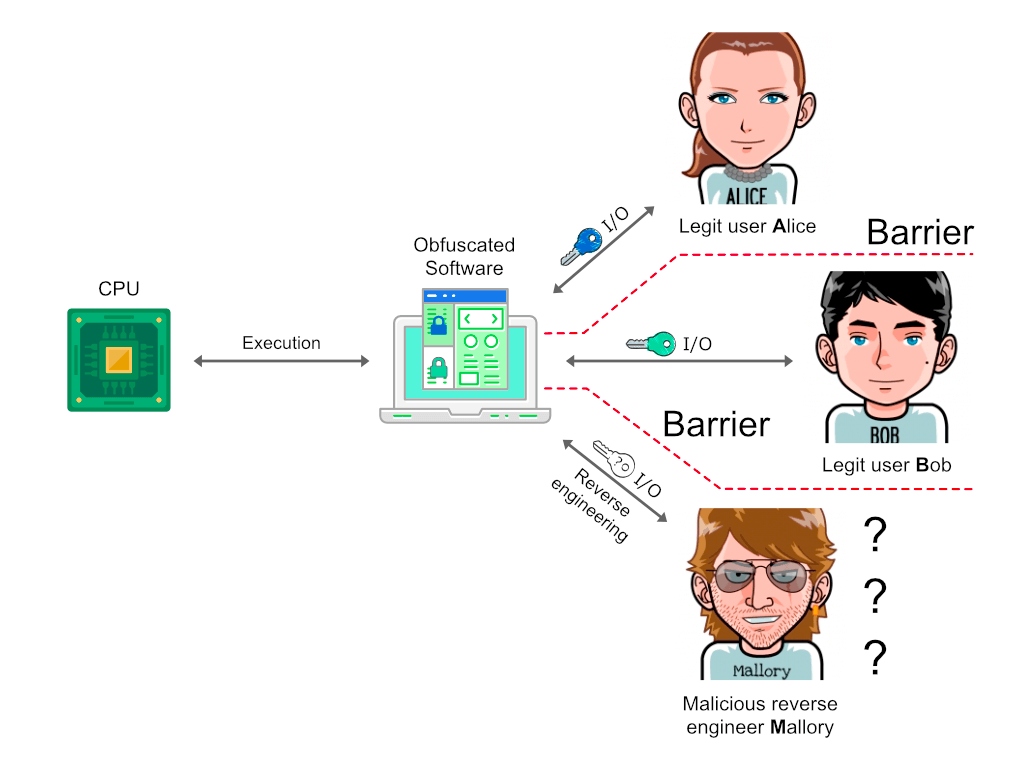Figure 4. Software obfuscation and interactions between participants
Note how natural security barriers appeared between participants once we identified that program input I can be a reliable source of key material for encryption of program parts.
Indeed, every user of an obfuscated program has its own set of unique input data. For example, if an obfuscated app (say, word processor) works on some files (say .doc files), an attacker cannot fully decompile the app unless he has all the possible file variations the app can work on. Which is not going to happen as an attacker cannot realistically have an access to all that data due to natural barriers of physical separation.
The conditional indistinguishability obfuscation (CiO) of software is now intuitively feasible. So it turns out that software obfuscation dilemma looks pretty solvable in terms of proposed model.
Realization
The intuitive feasibility of proposed CiO model would not mean a lot, unless at least one practical implementation is found.
The CiO model implies a conditional obfuscation, so we had to focus on conditional blocks of code, and specifically on predicates:
if (p)
DoSomething();
The conditional block should only be revealed when p is true. And we know that p should be tied to program input I somehow.
Thanks to the work described in paper "Indistinguishable Predicates: A New Tool for Obfuscation" by Zobernig et al. [Zobernig17], we focused our attention on evasive predicates.
An example of evasive predicate is a password check function p(x) = "x == pw". Since it is hard to find an input x that satisfies an evasive predicate, this class of predicates is a good candidate for obfuscation.
Initially we weren't sure if that was a possible endeavor, but on October 24, 2018 around 4 AM we came up with a plausible solution.
Let's take a look at the following code circuit:
if (x == C)
{
DoSomething();
…
}
where x == C is an evasive predicate with input x and constant C.
A good thing about homomorphic encryption is that it allows to view the data through the prism of equations. Note that our evasive predicate is an equation:
x == C
This fact allows us to apply a deterministic encryption function E to both sides:
E(x) == E(C)
Once encryption is applied, please note that E(C) can be calculated at compile time as constant CE = E(C), thus irreversibly hiding the original value of C:
E(x) == CE
As a result, we get an encrypted predicate p(x) that is perfectly functional at run time but never discloses the original value of C while providing us with 1 bit of unencrypted output:
p(x) = "E(x) == CE"
Unencrypted output eliminates the necessity of HE function D that would thwart the obfuscation otherwise. The elimination of D effectively transforms E to a trapdoor function.
So, now we have a conditional statement with a homomorphically encrypted predicate p(x):
if (E(x) == CE)
{
DoSomething();
…
}
An important observation is that x may or may not be tied to program input I. In order to find the exact relation of x to I, all program data flows would need to be traced. Such kind of tracing may be an enormous or even computationally impossible task. So let's just assume that x of every predicate is related to program input I with some not insignificant probability.
The next question is how to encrypt the conditional block of the if statement.
First of all, we need to ensure that the code of conditional block is translated to the data form:
BL = { DoSomething(); … }
if (E(x) == CE)
eval(BL);
Eazfuscator.NET achieves that by allowing homomorphic encryption only in virtualized methods, as the virtualized code is in data form already.
Secondly, we need to introduce another encryption function. Let's call it Es as it should be symmetric. Ds is a corresponding decryption function.
Then, we can use the predicate constant C as a key material for Es in order to encrypt the conditional block BL at compile time:
BLE = Es(BL, C)
Thanks to evasiveness of predicate, we can rely on the fact that x equals to C when the conditional block hits the execution path. In this way, the encrypted conditional block BLE can be revealed (decrypted) in run time when and only when x == C:
if (E(x) == CE)
eval(Ds(BLE, x));
The goal is achieved.
The obfuscated predicate is indistinguishable. The code of conditional block is also indistinguishable and can only be revealed when it hits the execution path. This behavior corresponds to the proposed model of conditional indistinguishability obfuscation (CiO).
Some Practical Examples
In accordance to original spirit of the product, Eazfuscator.NET automatically finds and indistinguishably obfuscates all the circuits that are suitable for homomorphic encryption (HE) in virtualized methods.
Currently it covers just one circuit class and integer data types, but we plan to significantly extend HE coverage in the future.
We quickly identified that customers will want to visualize the homomorphically encrypted regions of code. That's why we've built HE visualization tool right into Eazfuscator.NET 2019.3 extension for Visual Studio:
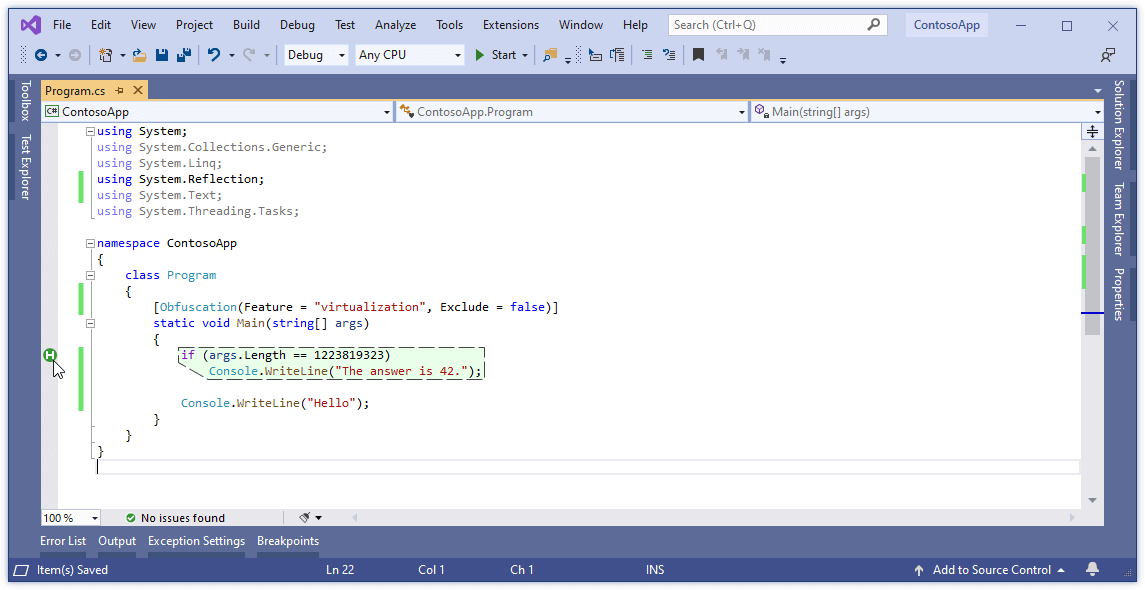Figure 5. Visualization of homomorphically encrypted regions of code
Whenever a suitable code circuit is found, a green circled H symbol appears at the left side of the editor. Hovering the mouse over that symbol reveals some useful information such as the boundaries of encrypted region and the number of entropy bits in key material.
What can it be used for?
HE is a tool, and your imagination is the driver. Here is an interesting quote from Kaspersky [Kris03]:
... trying the combinations of all [...] conceivable arguments will take an infinite amount of time. Reconstructing the source code of the program thus protected will not be possible before each of its branches gains control at least once. However, the frequency of calling different branches is not identical; it is very low for some of them. For example, a special handler can be installed for the word "pine" entered in the text editor. This handler may carry out some additional checks for integrity of the program code, or for the cleanliness of the license for the software being used.
The hacker will not be able to figure out whether the program is [fully] cracked and [will] end quickly. Careful and laborious testing will be necessary, but even carrying out this will not be [that] helpful.
Try It Yourself
Download Eazfuscator.NET and try HE on your own code.
DISCLAIMER: This research and discovery is property of public domain.
AUTHORS: Oleksiy Gapotchenko, Kirill Rode
ORGANIZATION: Gapotchenko LLC
LOCATION: Kharkiv
YEAR: 2019
References
[Barak01]
B. Barak and O. Goldreich and R. Impagliazzo and S. Rudich and A. Sahai and S. P. Vadhan and Ke Yang, “On the (im)possibility of obfuscating programs,” in Advances in Cryptology -- CRYPTO 2001, 21st Annual International Cryptology Conference, Santa Barbara, California, USA, August 19-23, 2001, Proceedings
[Kris03]
K. Kaspersky, “Hacker Disassembling Uncovered: Powerful Techniques To Safeguard Your Programming,” ISBN 978-1-931769-22-8, 2003
[Zobernig17]
L. Zobernig and S. D. Galbraith and G. Russello, “Indistinguishable Predicates: A New Tool for Obfuscation,” IACR Cryptology ePrint Archive, 2017
P.S. We aimed to use as few paragraphs as possible but the resulting article nevertheless have become rather large. More advanced topics like handling of low-entropy inputs, HE vs custom-built encrypted point functions, malleability and algebraic attacks, dictionary and replay attacks on a deterministic cryptosystem etc are thus omitted. They are subjects of a future, probably more formal publication.